The opposition to the fluid flow within the narrow channels of a microfluidic device causes pressure drop in fluidic systems. This drop arises from the viscous forces acting on the fluid as it moves through confined geometries, and is primarily determined by channel dimensions, shape, and the fluid's viscosity. Pressure drop in an incompressible and Newtonian fluid under laminar flow (Reynolds number less than 2300), inside a long tube of a constant cross-section can be approximated using the Hagen-Poiseuille equation:

\[ \Delta P = \frac{8 \pi \mu L Q}{A^2 } \] where:

\(\Delta P\) is the pressure difference between the two ends of the tube

\(\mu\) is dynamic viscosity

\(L\) is the length of the tube

\(Q\) is the volumetric flow rate

\(A\) is the cross-section of the tube or microfluidic feature

Microfluidic resistance (also known as hydraulic or flow resistance) characterizes a fluidic system and is independent of flow rate. It represents the pressure difference required to move a unit volume of liquid per unit time between two points in a channel:

\[ R = \frac{\Delta P}{Q } = \frac{8 \pi \mu L }{A^2 } \]

Pressure drop, flow rate, and microfluidic resistance are analogous to voltage, current, and resistance in electrical circuits. As such, Kirchhoff's laws can be applied to analyze complex microfluidic networks. To simplify the analysis, complex networks can be divided into simpler elements. For instance, the total pressure drop in a series of microfluidic channels with varying inner diameters can be calculated by summing the pressure drops across each section. This total pressure drop serves as a foundation for selecting instruments and designing systems that regulate flow rates, pressure, and fluid behavior. In parallel microchannel networks, the analysis involves dividing the total flow rate among the channels while considering their respective resistances.

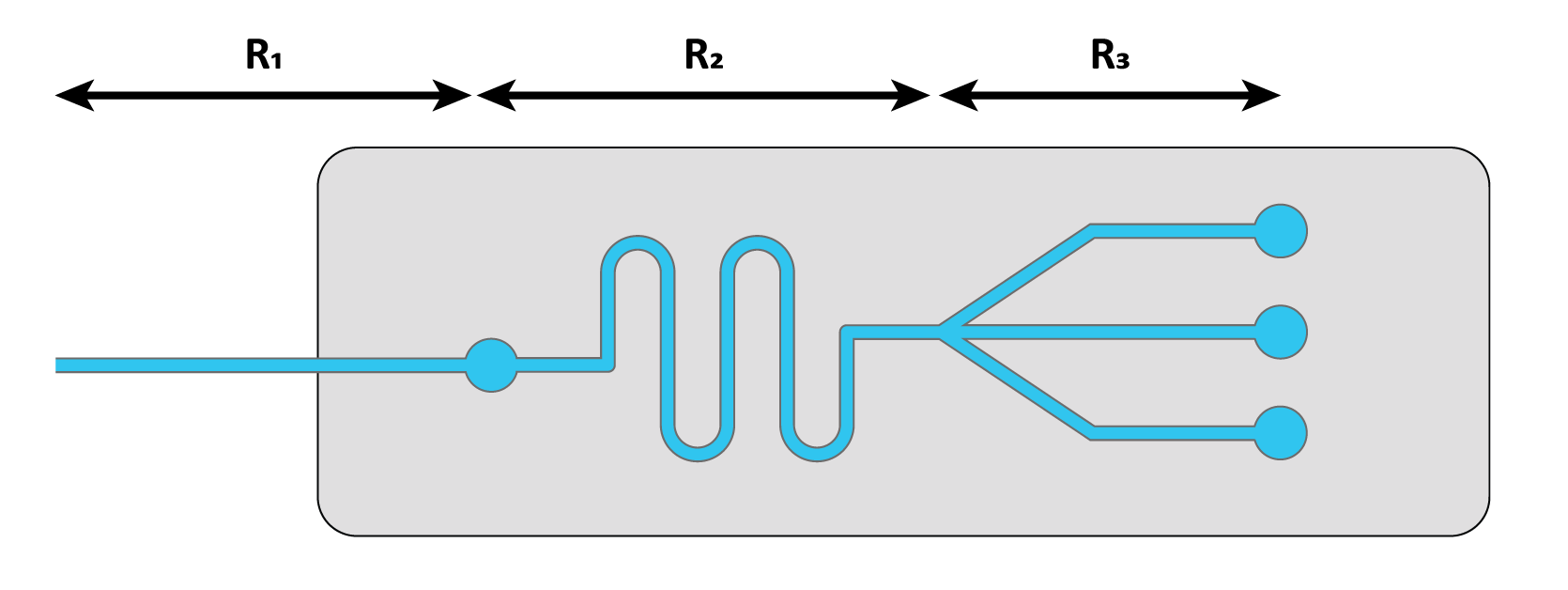
This calculator helps you determine the pressure drop along a tube with a constant inner diameter (ID). Additionally, you can select a rectangular cross-section to calculate the pressure drop and microfluidic resistance in channels with a rectangular cross-section.